Gradient Descent (GD) is the basic optimization algorithm for machine learning or deep learning. This post explains the basic concept of gradient descent with python code.
Parameter Learning
Data is the outcome of action or activity.
y, x
Our focus is to predict the outcome of next action from data. For this end, we should develop a model to describe data properly and do forecasting
Model is a function of data and parameters (θ= (w,b)′). We estimate parameters which fit data well.

Loss is a distance function between data and model like MSE(Mean Squared Error).

Since data is fixed and given, the learning is the parameter update.

Here γ is the learning rate or step size and  is the gradient. The gradient is the partial derivatives of J with respect to θ as follows.
is the gradient. The gradient is the partial derivatives of J with respect to θ as follows.

Illustration for Gradient Descent
Purpose of learning is to minimize a loss or cost function J with respect to parameters. This is done by finding gradient. But the gradient always points in the direction of steepest increase in the loss function as can be seen in the following figure.

Therefore the gradient descent which aims to find target parameters(b∗) takes a step in the direction of the negative gradient in order to reduce loss. For candidate parameters to move in the direction of reducing loss, new parameters are updated by negative gradient with learning rate or step size. In other words, parameters are determined by the gradient descent method automatically but learning rate is set by hand, which is a hyperparameter.
Python Code
The following python code implements the above explanation about gradient descent algorithm. Due to its structured simplicity, it is straightforward to understand relevant aspect of the gradient descent.
#=========================================================================#
# Financial Econometrics & Derivatives, ML/DL using R, Python, Tensorflow
# by Sang-Heon Lee
#
# https://shleeai.blogspot.com
#-------------------------------------------------------------------------#
# Gradient Descent example
#=========================================================================#
# -*- coding: utf-8 -*-
import numpy as np
#-------------------------------------------------------------------------#
# Declaration of functions
#-------------------------------------------------------------------------#
# Model
def Model(x, w, b):
y_hat = w*x + b
return y_hat
# Gradient
def Gradient(y,x,w,b):
y_hat = Model(x, w, b)
djdw = 2*np.mean((y-y_hat)*(-x))
djdb = 2*np.mean((y-y_hat)*(-1))
return djdw, djdb
# Learning : step = step size or learning rate
def Learning(y,x,w,b,lr):
djdw, djdb = Gradient(y, x, w, b)
w_update = w - step*djdw
b_update = b - step*djdb
return w_update, b_update
#-------------------------------------------------------------------------#
# use real data
#-------------------------------------------------------------------------#
import pandas as pd
import matplotlib.pyplot as plt
url = 'https://raw.githubusercontent.com/bammuger/blog/main/sample_data.csv'
data = pd.read_csv(url)
data.head()
plt.scatter(data.inputs, data.outputs, s = 0.5)
plt.show()
1) Sufficient Iteration
#-------------------------------------------------------------------------#
# Learning - sufficient iteration
#-------------------------------------------------------------------------#
# initial guess
w = 2; b = 3; step = 0.05
# Iternated learning process by parameter update using gradient descent
for i in range(0,5000):
y = data.outputs
x = data.inputs
w, b = Learning(y, x, w, b, step)
print("Learned_w: {}, Learned_b: {}".format(w, b))
X = np.linspace(0, 1, 100)
Y = w * X + b
plt.scatter(data.inputs, data.outputs, s = 0.3)
plt.plot(X, Y, '-r', linewidth = 1.5)
plt.show()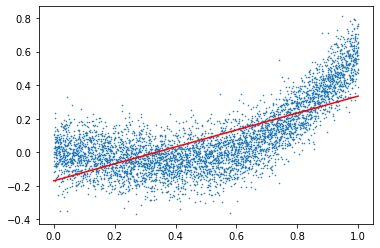
2) Insufficient Iteration
#-------------------------------------------------------------------------#
# Learning - insufficient iteration
#-------------------------------------------------------------------------#
# initial guess
w = 2; b = 3; step = 0.05
# Iternated learning process by parameter update using gradient descent
for i in range(0,10):
y = data.outputs
x = data.inputs
w, b = Learning(y, x, w, b, step)
print("Learned_w: {}, Learned_b: {}".format(w, b))
X = np.linspace(0, 1, 100)
Y = (w * X) + b
plt.scatter(data.inputs, data.outputs, s = 0.3)
plt.plot(X, Y, '-r', linewidth = 1.5)
plt.show()
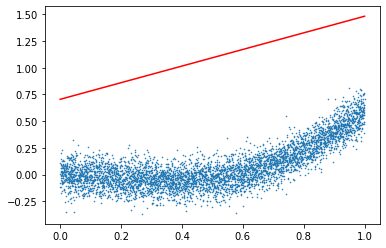
Next post, we will cover stochastic gradient descent, mini-batch gradient descent algorithm which are variants of GD.
Originally posted on SHLee AI Financial Model blog.
Disclosure: Interactive Brokers Third Party
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from SHLee AI Financial Model and is being posted with its permission. The views expressed in this material are solely those of the author and/or SHLee AI Financial Model and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.














Join The Conversation
For specific platform feedback and suggestions, please submit it directly to our team using these instructions.
If you have an account-specific question or concern, please reach out to Client Services.
We encourage you to look through our FAQs before posting. Your question may already be covered!