Excerpt
This post demonstrates the implementation of TensorFlow code for Variational Autoencoder (VAE) using a well-established example with MNIST digit data.
VAE in TensorFlow
Variational Autoencoder (VAE)
The Variational Autoencoder (VAE) is a generative model that allows us to learn a probabilistic representation of data.
The VAE architecture consists of an encoder and a decoder. The encoder maps input data to a probability distribution in a latent space, while the decoder generates data from samples drawn from the latent space.
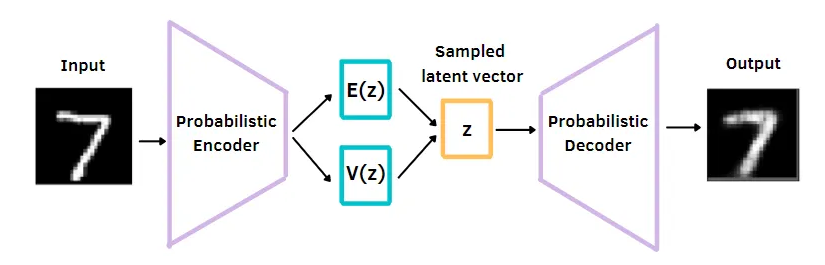
The core concept of VAE is the latent space, which is represented by the mean and variance of a Gaussian distribution. The equations for VAE are as follows:

The loss function for VAE includes a reconstruction loss and a regularization term to encourage the latent space to be normally distributed.
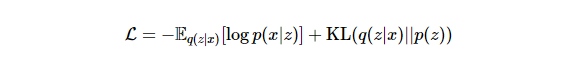
I’m omitting the derivation of the aforementioned loss function as there are abundant educational resources on Google. Numerous high-quality materials provide a better explanation than I can offer.
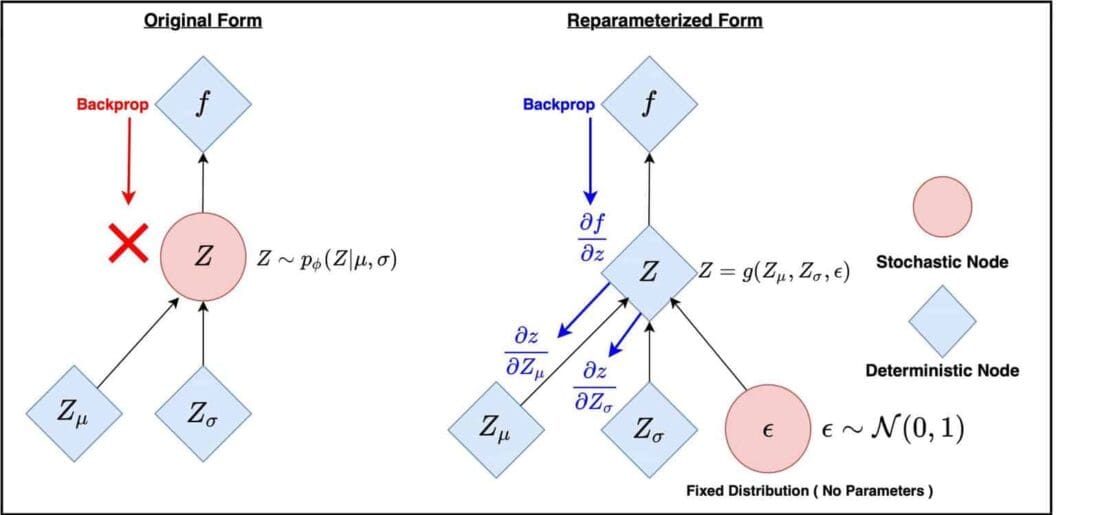
The reparameterization trick allows the training of generative models with stochastic elements while maintaining differentiability. It is crucial when working with continuous latent variables.
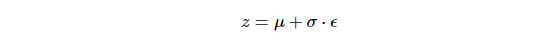
here, μ and σ are mean and standard deviation of the distribution of the latent variable z. ϵ is sampled from a fixed distribution, typically a standard Gaussian distribution, N(0,1).
Python Jupyter Notebook Code
A well-established example of VAE’s application is with MNIST digits. The following code reads MNIST data and performs some preprocessing.
import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import mnist
from keras.layers import Input, Lambda, Dense
from keras.models import Model
from keras import backend as K
from keras.utils import plot_model
from keras.losses import binary_crossentropy
# network parameters
rec_dim=784
input_shape = (rec_dim,)
int_dim = 512
lat_dim = 2
# Load the MNIST data
(x_tr, y_tr), (x_te, y_te) = mnist.load_data()
# normalize values of image pixels between 0 and 1f
x_tr = x_tr.astype('float32') / 255.
x_te = x_te.astype('float32') / 255.
# 28x28 2D matrix --> 784x1 1D vector
x_tr = x_tr.reshape((len(x_tr), np.prod(x_tr.shape[1:])))
x_te = x_te.reshape((len(x_te), np.prod(x_te.shape[1:])))
print(x_tr.shape, x_te.shape)The following code includes both the encoder and decoder. The encoder portion involves sampling latent factors using their mean and variance through the reparameterization trick.
#=======================
# Encoder
#=======================
# Z sampling function
def sampling(args):
z_mean, z_log_var = args
batch = K.shape(z_mean)[0]
dim = K.int_shape(z_mean)[1]
# Reparameterization Trick
# draw random sample ε from Gussian(=normal) distribution
# by default, random_normal has mean = 0 and std = 1.0
epsilon = K.random_normal(shape=(batch, dim))
return z_mean + K.exp(0.5 * z_log_var) * epsilon
# Input shape
inputs = Input(shape=input_shape)
enc_x = Dense(int_dim, activation='relu')(inputs)
z_mean = Dense(lat_dim)(enc_x)
z_log_var = Dense(lat_dim)(enc_x)
# sampling z
z_sampling = Lambda(sampling, (lat_dim,))([z_mean, z_log_var])
# encoder model has multi-output so a list is used
encoder = Model(inputs,[z_mean,z_log_var,z_sampling])
encoder.summary()
#=======================
# Decoder
#=======================
# Input of decoder is z
input_z = Input(shape=(lat_dim,))
dec_h = Dense(int_dim, activation='relu')(input_z)
outputs = Dense(rec_dim, activation='sigmoid')(dec_h)
# z is the input and the reconstructed image is the output
decoder = Model(input_z, outputs)
decoder.summary()After constructing the VAE model, which encompasses both the encoder and decoder, the VAE loss, also referred to as the Evidence Lower Bound (ELBO), is calculated as the combination of the reconstruction loss and the Kullback-Leibler (KL) loss. Notably, in the case of beta-VAE, the KL loss is adjusted using a scaling factor, beta, to strike a balance between these two components.
#=======================
# VAE model
#=======================
outputs = decoder(encoder(inputs)[2])
vae = Model(inputs, outputs)
#--------------------------------------------------
# VAE_loss = ELBO
#--------------------------------------------------
# (1)Reconstruct loss (Marginal_likelihood) : Cross-entropy
rec_loss = binary_crossentropy(inputs,outputs)
rec_loss *= rec_dim
# (2) KL divergence(Latent_loss)
kl_loss = 1 + z_log_var - K.square(z_mean) - K.exp(z_log_var)
kl_loss = -0.5*K.sum(kl_loss, 1)
# (3) ELBO
vae_loss = K.mean(rec_loss + kl_loss)
#--------------------------------------------------
vae.add_loss(vae_loss)
vae.compile(optimizer='adam')
vae.summary()
history = vae.fit(x_tr, x_tr, shuffle=True,
epochs=30, batch_size=64,
validation_data=(x_te, x_te))Visit SHLee AI Financial Model for details on how to visualize the training and validation losses across epochs.
Originally posted on SHLee AI Financial Model blog.
Disclosure: Interactive Brokers Third Party
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from SHLee AI Financial Model and is being posted with its permission. The views expressed in this material are solely those of the author and/or SHLee AI Financial Model and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.















Join The Conversation
For specific platform feedback and suggestions, please submit it directly to our team using these instructions.
If you have an account-specific question or concern, please reach out to Client Services.
We encourage you to look through our FAQs before posting. Your question may already be covered!