This post demonstrates the application of Differential Evolution (DE) to estimate Nelson-Siegel parameters using the NMOF R package.
Differential Evolution (DE)
Gilli et al. (2010) applied the Differential Evolution algorithm to the Nelson-Siegel (NS) or Nelson-Siegel-Svensson (NSS) model. The authors implemented and tested this optimization and showed that it is capable of reliably solving the numerical problem of the NS or NSS model.
This DE optimization algorithm can be used from the R package, NMOF, and the authors kindly provided the R code in the appendix of their working paper. This allowed me to apply this code to some data and verify that the estimation results match those obtained using existing algorithms such as the Nelder-Mead.
Following Gilli et al. (2010), there are two notational differences from what I have been accustomed to. First, maturity is expressed in years. Second, the time decay parameter is in reciprocal form, denoted as ![]() . Therefore, the NS model is represented as follow.
. Therefore, the NS model is represented as follow.
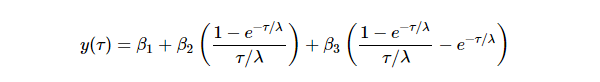
R code
The following R code estimates the Nelson-Siegel parameters by using the DE.
#========================================================#
# Quantitative Financial Econometrics & Derivatives
# ML/DL using R, Python, Tensorflow by Sang-Heon Lee
#
# https://shleeai.blogspot.com
#--------------------------------------------------------#
# Estimating the Nelson-Siegel model
# using Differential Evolution (DE)
#========================================================#
graphics.off(); rm(list = ls())
library(NMOF) # Differential Evolution
#-----------------------------------------------
# Objective function
#-----------------------------------------------
OF <- function(param, data) {
y <- data$model(param, data$tm)
maxdiff <- y - data$yM
# max absolute error
# maxdiff <- max(abs(maxdiff))
# Sum of Squares
maxdiff <- sum(maxdiff^2)
if (is.na(maxdiff))
maxdiff <- 1e10
maxdiff
}
#=======================================================
# 1. Read data
#=======================================================
# b1, b2, b3, lambda, RMSE for comparisons
ns_reg_para_rmse1 <- c(
4.26219396, -4.08609206, -4.90893865,
3.060792, 0.04883786)
ns_reg_para_rmse2 <- c(
4.97628654, -4.75365297, -6.40263059,
1.651215, 0.04157326)
str.zero <- "
mat rate1 rate2
3 0.0781 0.0591
6 0.1192 0.0931
9 0.1579 0.1270
12 0.1893 0.1654
24 0.2669 0.3919
36 0.3831 0.8192
48 0.5489 1.3242
60 0.7371 1.7623
72 0.9523 2.1495
84 1.1936 2.4994
96 1.4275 2.7740
108 1.6424 2.9798
120 1.8326 3.1662
144 2.1715 3.4829
180 2.5489 3.7827
240 2.8093 3.9696"
df <- read.table(text = str.zero, header=TRUE)
m <- df$mat
y1 <- df$rate1; y2 <- df$rate2
#=======================================================
# 2. Estimation
#=======================================================
#-------------------------------------------------------
# NS estimation with 1st data
#-------------------------------------------------------
data <- list(yM = y1, # percent
tm = m/12, # in years
model = NS,
ww = 0.1,
min = c( 0,-15,-30, 0),
max = c(15, 30, 30,10)
)
f_penalty <- function(mP, data) {
minV <- data$min
maxV <- data$max
ww <- data$ww
## if larger than maxV, element in A is positiv
A <- mP - as.vector(maxV)
A <- A + abs(A)
## if smaller than minV, element in B is positiv
B <- as.vector(minV) - mP
B <- B + abs(B)
# ## beta 1 + beta2 > 0
C <- ww*((mP[1L, ] + mP[2L, ]) - abs(mP[1L, ] + mP[2L, ]))
A <- ww * colSums(A + B) - C
A
}
algo <- list(nP = 100L, ## population size
nG = 500L, ## number of generations
F = 0.50, ## step size
CR = 0.99, ## prob. of crossover
min = c( 0,-15,-30, 0),
max = c(15, 30, 30,10),
pen = f_penalty,
repair = NULL,
loopOF = TRUE, ## loop over popuation? yes
loopPen = FALSE, ## loop over popuation? no
loopRepair = TRUE, ## loop over popuation? yes
printBar = FALSE)
set.seed(90)
deopt <- DEopt(OF = OF, algo = algo, data = data)
nsdtim_out1 <- c(deopt$xbest,
sqrt(deopt$OFvalue/length(m)))
#-------------------------------------------------------
# NS estimation with 2nd data
#-------------------------------------------------------
data$yM <- y2
f_penalty <- function(mP, data) {
minV <- data$min
maxV <- data$max
ww <- data$ww
## if larger than maxV, element in A is positiv
A <- mP - as.vector(maxV)
A <- A + abs(A)
## if smaller than minV, element in B is positiv
B <- as.vector(minV) - mP
B <- B + abs(B)
# beta 1 + beta2 > 0 is not applied
A <- ww * colSums(A + B)
A
}
# new penalty without beta 1 + beta2 > 0
algo$pen <- f_penalty
set.seed(90)
deopt <- DEopt(OF = OF, algo = algo, data = data)
nsdtim_out2 <- c(deopt$xbest,
sqrt(deopt$OFvalue/length(m)))
#=======================================================
# 3. Results and Comparisons
#=======================================================
ns_reg_para_rmse1
nsdtim_out1
ns_reg_para_rmse2
nsdtim_out2As can be seen in the following results, It seems that parameter estimates from the DE algorithm are the same as the benchmark results.
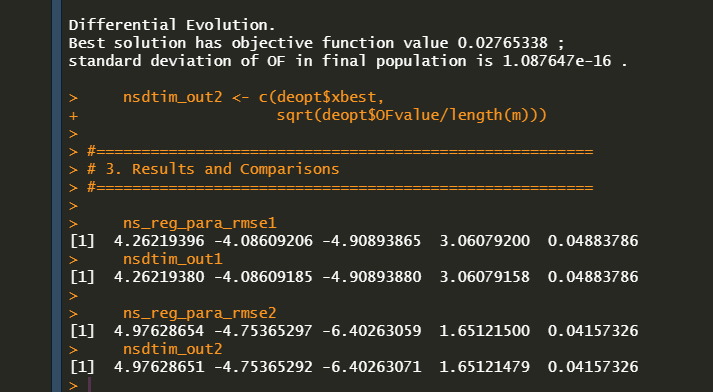
I believe this approach is highly effective in terms of avoiding local minima and achieving fast convergence.
Reference
Gilli, M., S. Große, and E. Schumann (2010). Calibrating the Nelson–Siegel–Svensson model. COMISEF Working Paper Series No. 31.
Originally posted on SHLee AI Financial Model blog.
Disclosure: Interactive Brokers Third Party
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from SHLee AI Financial Model and is being posted with its permission. The views expressed in this material are solely those of the author and/or SHLee AI Financial Model and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.















Join The Conversation
For specific platform feedback and suggestions, please submit it directly to our team using these instructions.
If you have an account-specific question or concern, please reach out to Client Services.
We encourage you to look through our FAQs before posting. Your question may already be covered!