Introduction to Options – The Greeks

The Options Greeks lesson is designed to familiarize traders with a set of risk factors used to monitor a portfolio’s profile (known as “The Greeks”). In this lesson, you will learn why some option prices are more or less responsive to changing prices in the value of the underlying security.

In this lesson, we will explain the definition of each of the Greek variables and explain to you, using an interactive options calculator, what influences days to expiration, interest rates, and the proximity between the option strike price and the price of the underlying have on the price of an option over time.

Risk Measures: Introduction

When option traders understand what basic inputs determine the pricing model, they are ready to move into dealing with option portfolio’s risk measures or “Greeks”. These risk variables are called “the Greeks” because, with the exception of Vega, each risk measure is represented by a letter of the Greek alphabet. The Greeks are dependent upon the inputs for an option’s pricing model.

This lesson assumes that the viewer is familiar with basic options risks, strategies and terminology.  As discussed in prior lessons, options trading provides additional leverage to trading equities, and thus carries increased risk.  Options involve risk and are not suitable for all investors. For more information read the “Characteristics and Risks of Standardized Options”. For a copy, call 312 542-6901. An option buyer can lose the entire premium. The option seller may have unlimited risk of loss.

This lesson incorporates an online options calculator from the Options Industry Council. It’s a free interactive resource available from OptionsEducation.org

Throughout this lesson we explain why each variable impacts the price of an options, and we use the calculator to illustrate those changes. Access the calculator to type the inputs on screen and note the change to call and put prices as you vary them.

Call Delta

Delta represents the theoretical change in an option’s price for a $1 change in the price of the underlying asset.

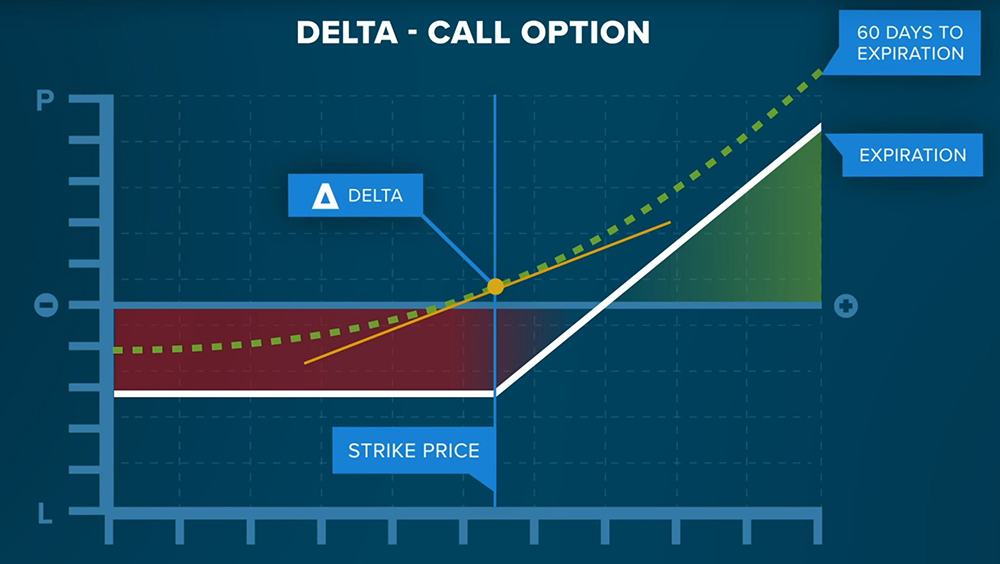For a call option, Delta will range from 0 to 1.  As the price of the underlying asset increases beyond the strike price and gets further in the money, the Delta will increase and approach 1, meaning that there is a greater change to the price of the option relative to the change in price of the underlying asset. An “at the money” option generally has a Delta of approximately 0.5. Alternatively, Delta can be thought of as the probability than an option will finish “in the money.”

Put Delta

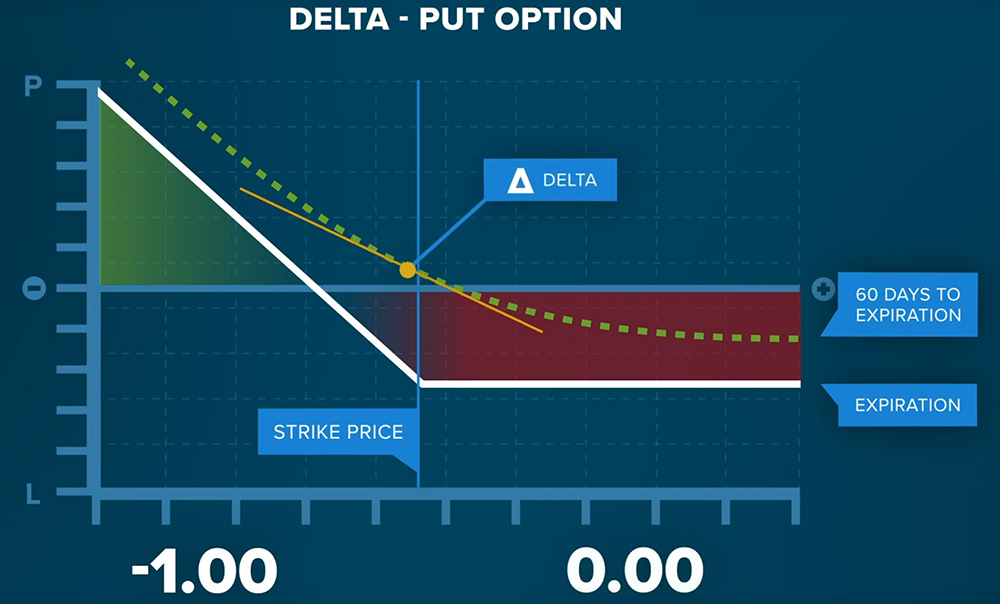
For a put option, Delta will range from -1 to 0.  As the price of the underlying asset decreases below the strike price and gets further in the money, the Delta will decrease and approach -1, meaning that there is a greater change to the price of the option relative to the change in price of the underlying asset An “at the money” option will have a Delta of -0.5. Alternatively, the Delta’s absolute value can also be thought of as the probability than an option will land “in the money”.

Delta Explanation

• As an example,  if the underlying asset price were to rise from $35.90 to $36.90 (a $1.00 increase), the average Delta would approximate the change in the option price.
• Underlying Price, Strike Price, Interest Rate, Volatility and Days to Expiration inputs will have an impact on the Delta. You can change the model inputs in the Options Calculator and click “Calculate” to better understand the impact of the model inputs on the Delta.

Gamma

• Gamma represents the rate of change of delta for a given change in the underlying asset’s price.
• Gamma is largest “at the money” and becomes smaller as options move further into or out of the money.
• The change in an option’s price (before expiration) is represented by a curved line and not a flat line.
• The Delta represents the change at any given point on the curved line, and the Gamma describes the change in the delta or curvature in the line.
• For calculus fans, it is the second order derivative. Understanding the Gamma in a portfolio is critical for a trader that is trying to continuously hedge a portfolio.

Gamma Explanation

• As an example, if the underlying asset price were to rise from $35.90 to $36.90 ($1.00), the old Delta plus the average Gamma would approximate the new Delta.
• Change the model inputs on the Options Calculator and click “Calculate” to better understand the impact of the model inputs on the Gamma.

Theta

Theta describes the relationship between time and the price of an option.

Theta only impacts the extrinsic value of an option. That’s because intrinsic value does not erode, it only moves with a change in the underlying asset price. As an option nears expiration, Theta will become increasingly negative.

Theta Explanation

The closer an option is to expiration, the less time value (extrinsic value) remains. Theta measures the approximate decline in an option’s premium due to the passage of time.  In other words, it measures that rate at which an option’s extrinsic value is declining.

Theta Calculator

Change the Options Calculator model inputs and click “Calculate” to better understand the impact of the model inputs on the Theta.

Vega

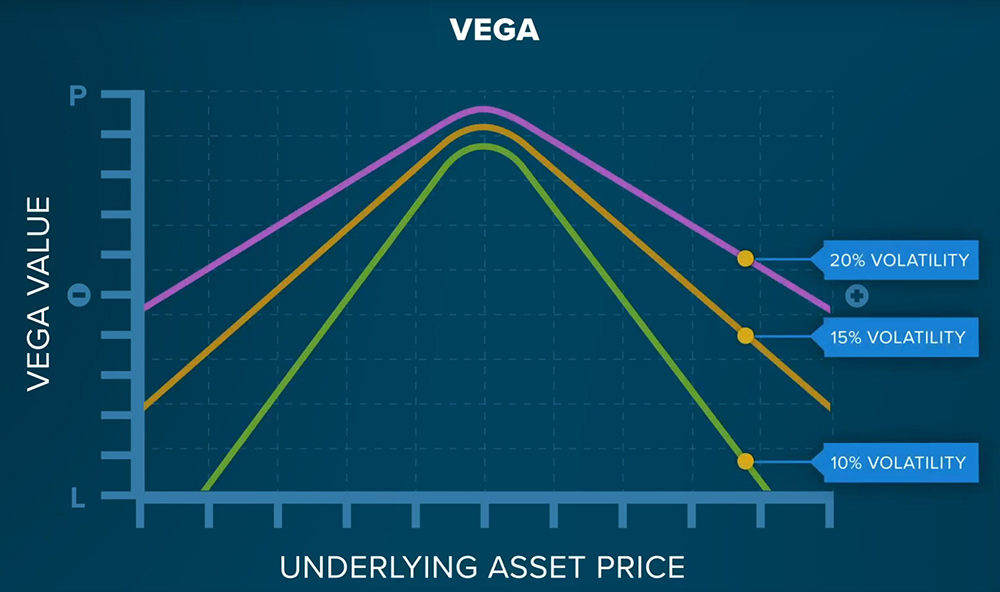
Vega represents the change in an option’s price due to a change in its implied volatility. Vega is always greatest for an “at the money” option and decreases as the underlying asset price moves increasingly “into the money” or “out of the money.”

Vega Explanation

An increase in volatility of 1% will change the option’s price by approximately the average of the Vega.

Vega Calculator

Change the model inputs on the Options Calculator and click “Calculate” to better understand the impact of the model inputs on the Vega.

Rho Definition

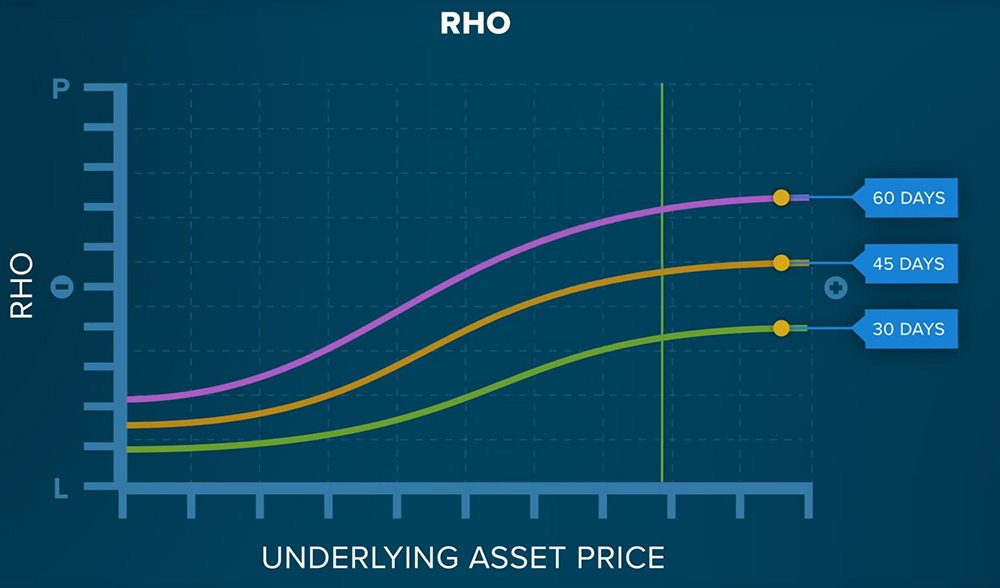
Rho represents an option’s price sensitivity to interest rates. The greater the underlying asset price and remaining days to expiration, the greater the Rho.

Rho Explanation

As an example, if the interest rate were to rise from 3.5% to 4.5%, the average value of Rho would approximate the change in the option’s price.

Rho Calculator

Change the model inputs on the Options Calculator and click “Calculate” to better understand the impact of the model inputs on the Rho.

Putting it Together: Price Model

Now let’s put it all together. Using the following assumptions, we can see the estimated value of a call option.

• Let’s use a Share Price of $35.90,
• A Strike Price of $40.00,
• And assume an Interest Rate of 4 percent,
• Let’s assume an Implied Volatility reading of 38.8% for the underlying,
• And say the option contracts has 38 days to expire.
• The Call Price works out to be almost 54-cents ($0.5388).

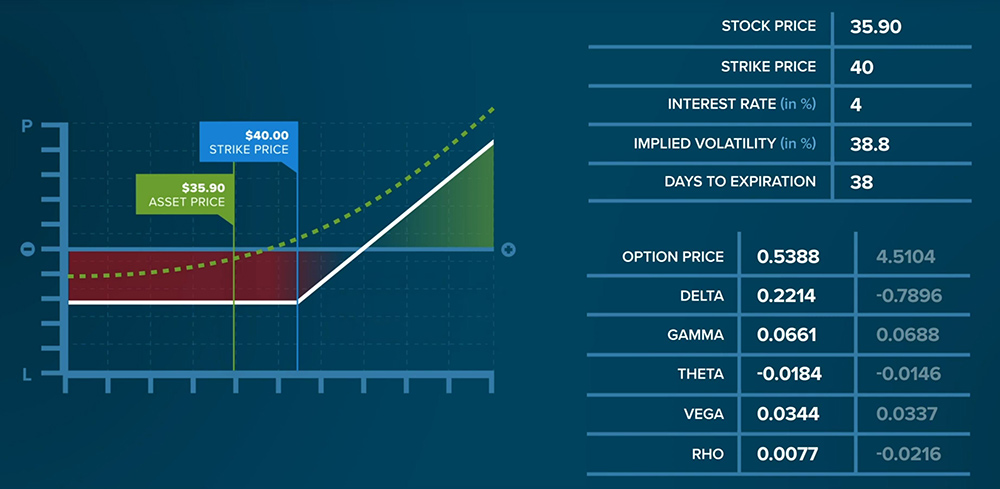Delta

The measure returned for Delta is 0.2214. This means that for every $1.00 move in the underlying asset’s price the option value will change by approximately 22-cents (ignoring the impact of Gamma). Alternatively, there is a 22% chance that the option will expire at or above the strike price of $40.00.

Gamma

The Gamma reading of 0.0661 tells us that should the underlying price rise by $1.00, then Delta will rise by approximately 6.6 cents, because of the curvature in the option’s price line.

Theta

The reading of  -0.0184 for Theta tells us that the value of the option contract drops approximately 1.8 cents for each day that passes.

Vega

The Vega of 0.0344 tells us that if implied volatility were to increase from 38.8% to 39.8%, then the value of the option would increase by approximately 3.4 cents.

Rho

The reading of 0.0077 for Rho tells us that if interest rates were to increase from 4% to 5%, the option’s value would increase by approximately 0.77 cents.

Options Calculator

Now that we have covered the Greek risk factors, we encourage you to play with the free OIC Options Calculator to understand how changes in all of the inputs are likely to affect an option’s price and Greeks. It should be noted that inputs rarely change in isolation and so it is important to test the changing multiple inputs at the same time.