The post “Trend-Following Filters – Part 2/2” first appeared on Alpha Architect Blog.
1. Introduction
Part 1 of this analysis, which is available here, examines filters modeled on second-order processes from a digital signal processing (DSP) perspective to illustrate their properties and limitations. To briefly recap, a time series based on a second-order process consists of a mean a and a linear trend b which is contaminated with random normally distributed noise ε(t) where ε(t) ~ N(0, σε2):
- second-order process – mean a and linear trend b: x(t) = a + b*t + ε(t)
The filters analyzed in Part 1 include double moving average, double linear weighted moving average, double exponential smoothing, and alpha-beta tracking filters. Part 2 extends the analysis to filters modeled on third-order processes. A third-order process consists of a mean a, a linear trend b, and a quadratic trend c which is contaminated with random normally distributed noise ε(t):
- third-order process – mean a, linear trend b, and quadratic trend c: x(t) = a + b*t + ½*c*t2 + ε(t)
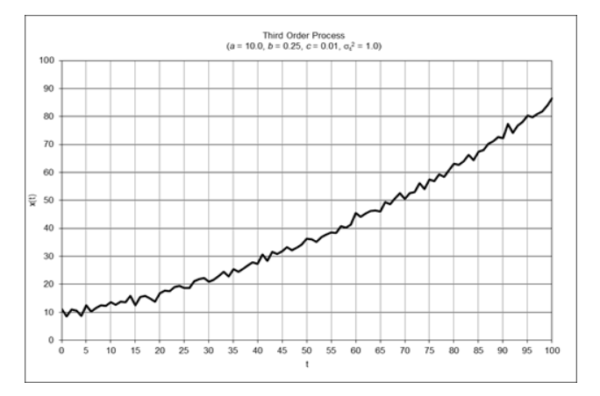
The filters analyzed are triple moving average, triple linear weighted moving average, triple exponential smoothing, and alpha-beta-gamma tracking filters. Note: This article assumes familiarity with Part 1 and also with the characteristics of financial time series and the digital signal processing concepts discussed in “An Introduction to Digital Signal Processing for Trend Following”, which is available here.
2. Triple Moving Average (TMA)
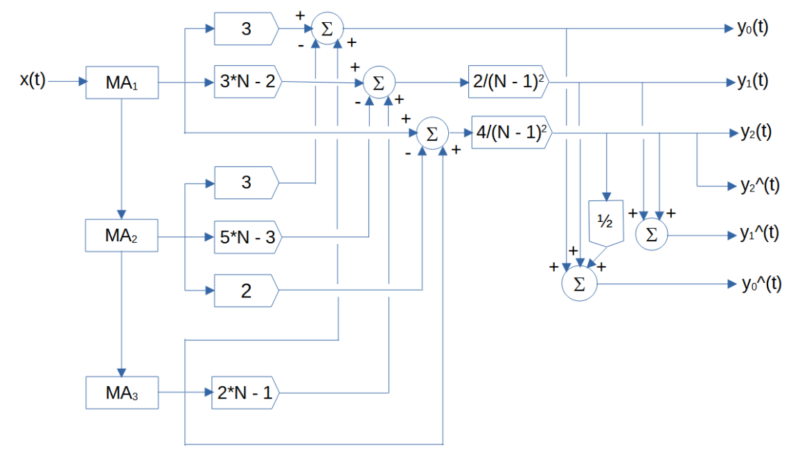
Triple moving average (TMA) is a time series estimation and process control method that uses three single moving averages to estimate time series that contain linear and quadratic trends 1. The triple moving average set of equations is:

where N is the number of input data points, i.e., the moving average length N (N > 1), included in the three single moving averages used to calculate the triple moving average, and x(t) represents the price at integer time t.
The triple moving average generates five main outputs: an estimate of the mean y0(t) at time step t, an estimate of the linear trend y1(t) at time step t, an estimate of the quadratic trend y2(t) at time step t, a mean expectation y0^(t) made at time step t for the next time step t+1, and a linear trend expectation y1^(t) made at time step t for the next time step t+1. The quadratic trend expectation y2^(t) for the next time step t+1 is the same as the quadratic trend estimate y2(t) since a triple moving average does not model cubic and higher-order trends.
Visit Alpha Architect to learn more about Triple Moving Average Mean Filter Frequency Response (N = 10).
Notes:
- Brown, R. G., Smoothing, Forecasting, and Prediction of Discrete Time Series, Prentice Hall, 1962.
- Brown, R. G., Smoothing, Forecasting, and Prediction of Discrete Time Series, Prentice Hall, 1962.
Disclosure: Alpha Architect
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
This site provides NO information on our value ETFs or our momentum ETFs. Please refer to this site.
Disclosure: Interactive Brokers Third Party
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from Alpha Architect and is being posted with its permission. The views expressed in this material are solely those of the author and/or Alpha Architect and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.















Join The Conversation
For specific platform feedback and suggestions, please submit it directly to our team using these instructions.
If you have an account-specific question or concern, please reach out to Client Services.
We encourage you to look through our FAQs before posting. Your question may already be covered!