The article “The Mathematics of Bonds: Simulating the Returns of Constant Maturity Government Bond ETFs” first appeared on Portfolio Optimizer blog.
Excerpt
With more than $1.2 trillion under management in the U.S. as of mid-July 20221, investors are more and more using bond ETFs as building blocks in their asset allocation.
One issue with such instruments, though, is that their price history dates back to at best 20021, which is problematic in some applications like trading strategy backtesting or portfolio historical stress-testing.
In this post, which builds on the paper Treasury Bond Return Data Starting in 1962 from Laurens Swinkels2, I will show that the returns of specific bond ETFs – those seeking a constant maturity exposure to government-issued bonds – can be simulated using standard textbook formulas2 together with appropriate yields to maturity.
This allows in particular to extend the price history of these ETFs by several tens of years thanks to publicly available yield to maturity series published by governments, government-affiliated agencies, researchers…
Notes:
- A Google sheet corresponding to this post is available here
Mathematical preliminaries
Bond yield formula
In what comes next, I will make heavy use of the formula expressing the price of a bond as a function of its yield to maturity.
This formula can be found in the appendix A3.1 Yield to maturity for settlement dates other than coupon payment dates of Tuckman and Serrat3, and is reproduced below for convenience.
Let be a bond4 at a date t, with a remaining maturity equal to T, a yield to maturity equal to yt and a coupon rate equal to ct.
Then, its price Pt(ct,yt,T) per 100 face amount is equal to
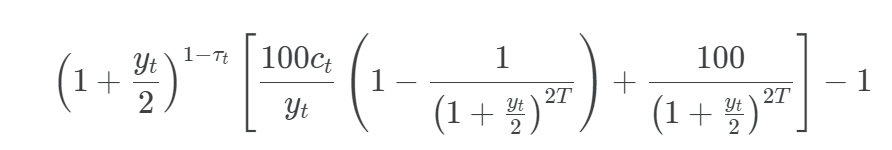
, where τt is the fraction of a semiannual period until the next coupon payment.
Par bond total return formula
Using the bond yield formula, it is possible to approximate the total return TR of a par bond over a specific period using only its remaining maturity at the beginning of the period, its yield to maturity at the beginning of the period and its yield to maturity at the end of the period.
Par bond total return formula for a monthly period
In the case of a monthly period, let be a bond such that:
—Its remaining maturity at the end of the month t−1 is equal to T.
—Its yield to maturity at the end of the month t−1, for a remaining maturity equal to T, is yt−1
—Its yield to maturity at the end of the month t, for a remaining maturity equal to T, is yt
Then, assuming that
—The bond trades at par at the end of the month t−1
—The bond yield curve at the end of the month t is flat for remaining maturities between 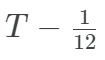 and T.
and T.
, the total return TRt of this bond from the end of the month t−1 to the end of the month t can be approximated by
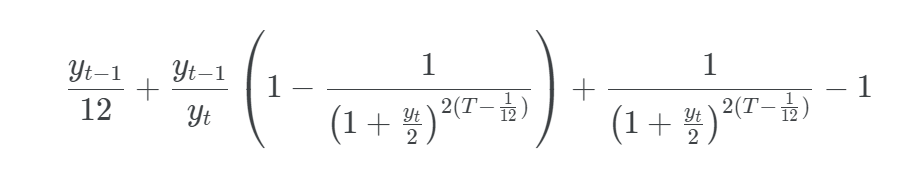
Demonstration of the par bond total return formula for a monthly period
A possible demonstration for the previous formula goes as follows.
At the end of the month t−1, the bond has the following characteristics:
— Its remaining maturity is equal to T
— Its coupon rate ct−1 is equal to its yield to maturity yt−1, because of the assumption that the bond trades at par at the end of the month t−1
Its price Pt−1(ct−1,yt−1,T) is then equal, through the bond yield formula

, with τt−1 the fraction of a semiannual period until the next coupon payment at the end of month t−1.
At the end of the month t, the bond has the following characteristics:
— Its remaining maturity is equal to 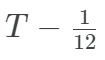 , one month short of its initial remaining maturity T
, one month short of its initial remaining maturity T
— Its coupon rate ct is equal to ct−1, that is, its initial yield to maturity yt−1
— Its yield to maturity is equal to yt, because of the assumption on the bond yield curve at the end of the month t
Its price 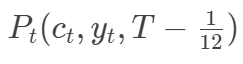 is then equal, through the bond yield formula, to
is then equal, through the bond yield formula, to
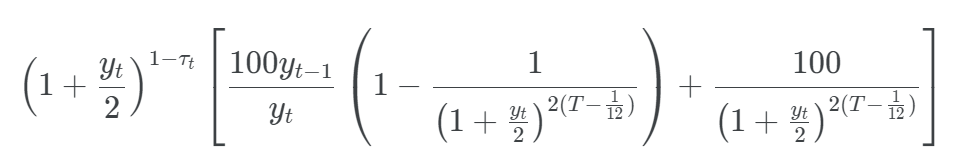
, with τt the fraction of a semiannual period until the next coupon payment at the end of month t.
The total return TRt of this bond from the end of the month t−1 to the end of the month t is then by definition equal to
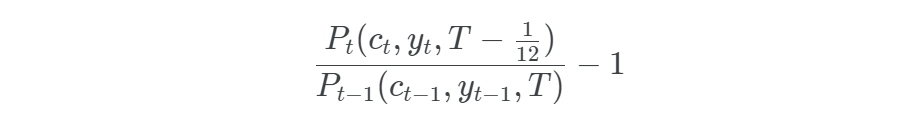
, that is
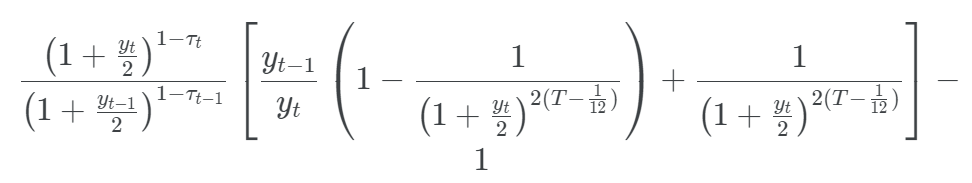
The first term of this expression corresponds to the re-investment of the accrued interest.
Under the practical assumptions that
— There is only a single rate for accrued interest, chosen equal to yt−15
— The accrued interest is not re-invested6
and noticing that 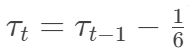 7, this expression becomes
7, this expression becomes
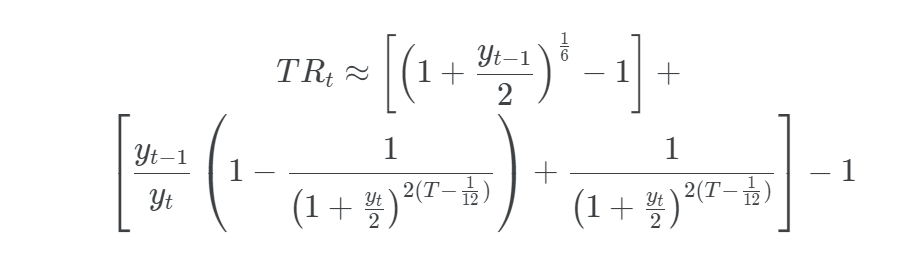
Finally, by linearizing the accrued interest through the first-order Taylor approximation 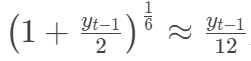 , this expression becomes
, this expression becomes
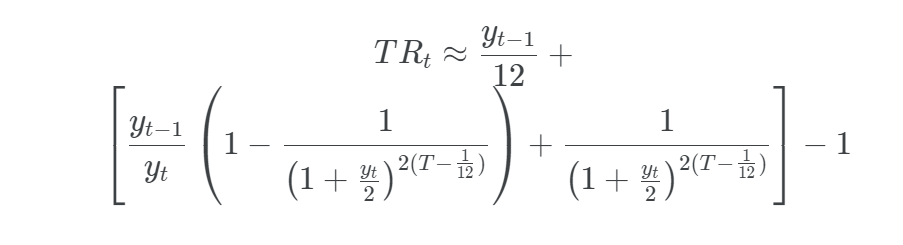
Remark:
The formula above is based on a suggestion by Dr Winfried Hallerbach to improve the accuracy of the initial formula used in Swinkels2 which is based on a second-order Taylor approximation of the bond yield formula, c.f. Swinkels8.
- See Happy 20th Anniversary of Bond ETFs. ↩ ↩2
- See Swinkels, L., 2019, Treasury Bond Return Data Starting in 1962, Data 4(3), 91. ↩ ↩2 ↩3 ↩4 ↩5 ↩6 ↩7 ↩8 ↩9 ↩10 ↩11 ↩12 ↩13 ↩14 ↩15
- See Tuckman, B., and Serrat A., 2022, Fixed Income Securities Tools for Today’s Markets, 4th edition, John Wiley And Sons Ltd. ↩
- In this post, I use the same conventions as in Tuckman and Serrat3: bonds are assumed to be paying semiannual coupons, their coupon rate is assumed to be annual, their yield to maturity is assumed to be provided as semiannually compounded and their maturity is assumed to be expressed in years. ↩
- Another sensible choice would be to use a rate equal to −1+22yt−1+yt. ↩
- Since bonds with semi-annual coupons are paying coupons every six months, these coupons are anyway hardly collected and re-invested every month in practice, so that this is a sensible simplifying assumption. ↩
- C.f. Tuckman and Serrat3 for explanations about the term 1661. ↩
- See Swinkels, L., 2023, Historical Data: International monthly government bond returns, Erasmus University Rotterdam (EUR). ↩
Visit Portfolio Optimizer blog to read the full article.
Disclosure: Interactive Brokers Third Party
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from Portfolio Optimizer and is being posted with its permission. The views expressed in this material are solely those of the author and/or Portfolio Optimizer and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.
Disclosure: ETFs
Any discussion or mention of an ETF is not to be construed as recommendation, promotion or solicitation. All investors should review and consider associated investment risks, charges and expenses of the investment company or fund prior to investing. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.















Join The Conversation
For specific platform feedback and suggestions, please submit it directly to our team using these instructions.
If you have an account-specific question or concern, please reach out to Client Services.
We encourage you to look through our FAQs before posting. Your question may already be covered!