Multiple Linear Regression using Tensorflow

This post implements the standard matrix based estimation of multiple linear regression model using Tensorflow. With this example, we can learn some basic vector or matrix operations in Tensorflow and also Python.

Linear Regression using Tensorflow

To study some basic vector or matrix operations in Tensorflow which is not familiar to us, we take the linear regression model as an example, which is familiar to us.

Linear Regression model

Multiple linear regression model has the following expression. (t = 1, 2,…, n)

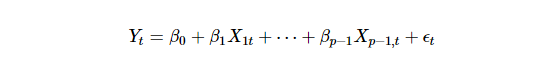
Here Y_t is the dependent variable and X_t=(1,X_1t,X_2t,…,X_p−1,t) is a set of independent variables. β=(β₀,β₁,β₂,…,β_p−1) is a vector of parameters and ϵ_t is a vector or stochastic disturbances.

It is worth noting that the number of parameters is p and the number of variables is p−1

Stochastic error term ϵ_t  is assumed in the following way.

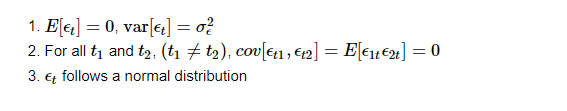
Least Squares Estimator

To estimate the regression coefficients β, we use least squares which minimize the sum of squared residuals. In a matrix notation, the least squares estimator is calculated in the following way.

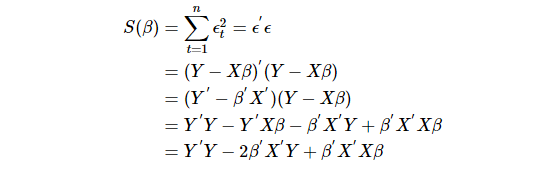
Differentiating S(β) with respect to β and set to zero results in the following the normal equation.

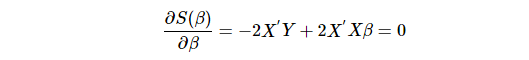
Hence the least squares estimator of β is

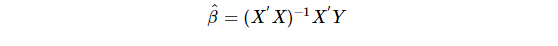
Standard Errors

follows the following distribution

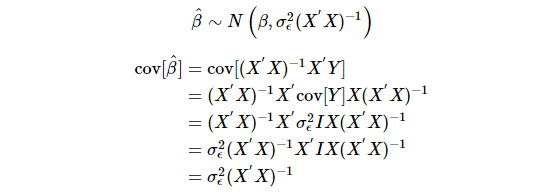
Since is the population parameter we don’t know, is replaced with the sample estimate of

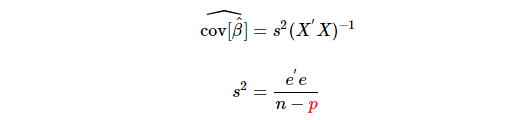
To estimate we need to estimate p parameters (1 intercept + (p-1) coefficients),in other words, p degree of freedom is lost.

Python code using Tensorflow

The purpose of this post is to learn some basic vector or matrix operations (matrix multiplication, transpose, inverse, etc.) in Tensorflow. As an example, we use the diabetes data from sklearn package which has 10 explanatory variables and 1 response variable.

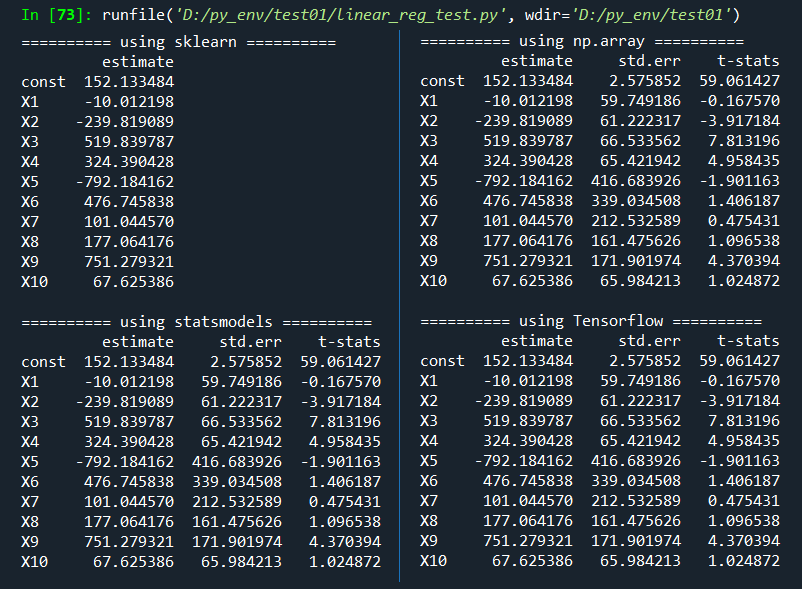
To check the estimation accuracy, regression outputs from sklearn, statsmodels are also considered. pd.DataFrame() from pandas package is used for make a table from np.array or Tenslorflow objects.

# -*- coding: utf-8 -*-
"""
#========================================================#
# Quantitative ALM, Financial Econometrics & Derivatives 
# ML/DL using R, Python, Tensorflow by Sang-Heon Lee 
#
# https://kiandlee.blogspot.com
#--------------------------------------------------------#
# Linear Regression model using Tensorflow 
#========================================================#
"""
 
import pandas as pd
import numpy as np
from sklearn import datasets, linear_model
 
"""""""""""""""""""""""""""""""""""""""""""""""""""
  Load the diabetes dataset
"""""""""""""""""""""""""""""""""""""""""""""""""""
X, y = datasets.load_diabetes(return_X_y=True)
nrow, ncol = X.shape; print (nrow, ncol) 
nparam = ncol+1 # number of parameters
 
v_row_name = np.hstack(
    [["const"], ["X"+str(i) for i in range(1,ncol+1)]])
 
 
"""""""""""""""""""""""""""""""""""""""""""""""""""
  1) using sklearn
"""""""""""""""""""""""""""""""""""""""""""""""""""
reg_mod = linear_model.LinearRegression() # object
reg_mod.fit(X, y) # estimation or tradining
 
df_out_sk = pd.DataFrame(
    np.hstack([reg_mod.intercept_, reg_mod.coef_]))
df_out_sk.columns = ["estimate"]
df_out_sk.index   = v_row_name
print("\n========== using sklearn ==========")
print(df_out_sk)
 
 
"""""""""""""""""""""""""""""""""""""""""""""""""""
  2) using statsmodels
"""""""""""""""""""""""""""""""""""""""""""""""""""
import statsmodels.api as sm
Xw1 = sm.add_constant(X)
ols = sm.OLS(y, Xw1)
fit = ols.fit()
#print(fit.summary())
 
df_out_ss = pd.DataFrame(np.vstack([fit.params, 
                fit.bse, fit.params/fit.bse]).T)
df_out_ss.columns = ["estimate", "std.err", "t-stats"]
df_out_ss.index   = v_row_name
 
print("\n========== using statsmodels ==========")
print(df_out_ss)
 
 
"""""""""""""""""""""""""""""""""""""""""""""""""""
  3) using matrix formula (np.array)
"""""""""""""""""""""""""""""""""""""""""""""""""""
mX    = np.column_stack([np.ones(nrow),X])
beta  = np.linalg.inv(mX.T.dot(mX)).dot(mX.T).dot(y)
err   = y - mX.dot(beta)
 
s2    = err.T.dot(err)/(nrow-ncol-1)
cov_beta = s2*np.linalg.inv(mX.T.dot(mX))
std_err  = np.sqrt(np.diag(cov_beta))
 
df_out_np = pd.DataFrame(
    np.row_stack((beta, std_err, beta/std_err)).T)
df_out_np.columns = ["estimate", "std.err", "t-stats"]
df_out_np.index   = v_row_name
 
print("\n========== using np.array ==========")
print(df_out_np)
 
 
"""
#==================================================
# 4) using matrix formula (Tensorflow)
#==================================================
"""
import tensorflow as tf
 
# from np.array
y = tf.constant(y, shape=[nrow, 1]) 
X = tf.constant(X, shape=[nrow, ncol])
 
# need double tensor
one  = tf.cast(tf.ones([nrow, 1]), tf.float64)
oneX = tf.concat([one, X], 1); # 1, X
 
XtX  = tf.matmul(oneX, oneX ,transpose_a=True)
Xty  = tf.matmul(oneX, y  ,transpose_a=True)
beta = tf.matmul(tf.linalg.inv(XtX),Xty)
err  = y - tf.matmul(oneX, beta)
s2   = tf.matmul(err, err, transpose_a=True)/(nrow-nparam)
cov_beta = s2*tf.linalg.inv(XtX)
std_err  = tf.sqrt(tf.linalg.diag_part(cov_beta))
beta = tf.reshape(beta,[nparam])
 
est_out   = tf.stack([beta, std_err, beta/std_err],1)
df_out_tf = pd.DataFrame(np.asarray(est_out))
df_out_tf.columns = ["estimate", "std.err", "t-stats"]
df_out_tf.index   = v_row_name
 
print("\n========== using Tensorflow ==========")
print(df_out_tf)

We can easily find that all results are the same as expected. In particular, two approaches using np.array and Tensorflow has the nearly same structure.

Concluding Remarks

This post dealt with how to use some basic vector or matrix operations of Tensorflow. It is similar to that of np.arrary but there are some subtle differences about manipulating array objects. Based on these, if we know remaining subjects such as for-loop, function definition, and optimization, it is expected that we can implement state space model using Kalman filter and estimate its parameters.

Originally posted on SH Fintech Modeling blog.