See Part I for an overview of the linear models and the concept of “regression”.
Nomenclature
When we read and learn about regression (and econometrics), every term or concept goes by a variety of names.
Visit QuantInsti website to view the complete Nomenclature table Vivek Krishnamoorthy has created: https://blog.quantinsti.com/linear-regression/#nomenclature
Types of linear regression
1. Simple linear regression
Imagine that we hold the Coca-Cola (NYSE : KO) stock and are interested in its returns. Conventionally, we denote our variable of interest with the letter YY. We usually have multiple observations (taken to be nn) of it. So, the YY that we previously mentioned is an n-dimensional vector containing values YiYi.
Here and throughout this post, I use the scalar versions of the equations. You can refer to this section to view the matrix forms. You can also read a more detailed treatment of the analytical expressions and derivations in standard econometric textbooks like Baltagi (2011), Woolridge (2015) and Greene (2018).
We want to examine the relationship between our stock’s returns(Y) and the market returns(denoted as X). We believe the market returns i.e. the SPDR S&P 500 ETF (NYSEARCA : SPY) should tell us something about KO‘s returns. For each observation i,
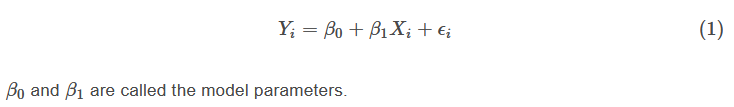
Equation 1 is just a dolled-up version of y=mx+c that we’d seen earlier with an additional ϵi term. In it β0 and β1 are commonly referred to as the intercept and the slope respectively.
This is the simple linear regression model.
We call it simple, since there is only one explanatory variable here; and we call it linear, since the equation is that of a straight line. It’s easy for us to visualize it in our mind’s eye since they are like the X– and Y -coordinates on a Cartesian plane.
A linear regression is linear in its regression coefficients.
A natural extension to this model is the multiple linear regression model.
Stay tuned for the next installment in which Vivek will discuss multiple linear regression.
Visit QuantInsti for additional insight on this topic: https://blog.quantinsti.com/linear-regression/.
Disclaimer: All investments and trading in the stock market involve risk. Any decisions to place trades in the financial markets, including trading in stock or options or other financial instruments is a personal decision that should only be made after thorough research, including a personal risk and financial assessment and the engagement of professional assistance to the extent you believe necessary. The trading strategies or related information mentioned in this article is for informational purposes only.
Any trading symbols displayed are for illustrative purposes only and are not intended to portray recommendations.
Disclosure: Interactive Brokers Third Party
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from QuantInsti and is being posted with its permission. The views expressed in this material are solely those of the author and/or QuantInsti and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.














Join The Conversation
For specific platform feedback and suggestions, please submit it directly to our team using these instructions.
If you have an account-specific question or concern, please reach out to Client Services.
We encourage you to look through our FAQs before posting. Your question may already be covered!