See Part I for an overview of Dijkstra algorithm.
Pseudo code of Dijkstra algorithm
The pseudo code of Dijkstra algorithm is:
function Dijkstra(L[1..n, 1..n]): matrix [2..n]
matrix D[2..n]
{initialization}
C <- {2, 3, …, n} {S = N \ C exists only implicitly}
for i ← 2 to n do D[i] ← L[1, i]
{greedy loop}
repeat n - 2 times
v ← some element of C that minimizes D[v]
C ← C \ {v} {and implicitly S ← S U {v}}
for each w ∈ C do
D[w] ← min(D[w], D[v] + L[v, w])
Return DPseudo code.py hosted with ❤ by GitHubDijkstra algorithm table
Assume the following routed graph:
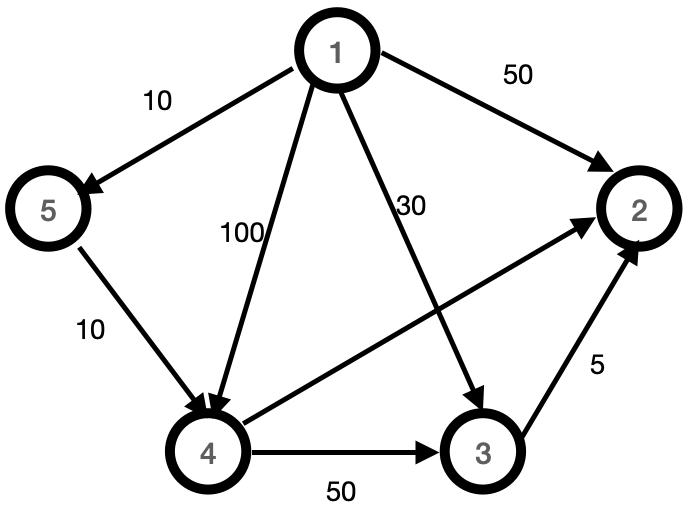
Dijkstra algorithm table
| Step | v | C | D |
| Initialization | – | {2, 3, 4, 5} | [50, 30, 100, 10] |
| 1 | 5 | {2, 3, 4} | [50, 30, 20, 10] |
| 2 | 4 | {2, 3} | [40, 30, 20, 10] |
| 3 | 3 | {2} | [35, 30, 20, 10] |
Obviously the matrix D would not change if we did one more interaction to remove the last element of C {2} and for this reason the main loop only repeats n-2 times.
Dijkstra algorithm time complexity
The initialisation requires a matrix L[1..n, 1..n] and therefore requires a time that is in the Order of n O(n)
The repeat loop requires looping through all the elements of C, so the total time is in the order of n2.O(n2)n2.O(n2)
The loop for each requires looping through all the elements of C, so the total time is on the order of n2.O(n2)n2.O(n2)
Therefore, the simple implementation of the Dijkstra algorithm requires a runtime that is O(n2)O(n2)
Depending on the implementation of the algorithm and as long as the number of edges is much smaller than n2n2, we can improve the complexity up to O((a + n) log n) if the graph is connected and is in O(a log n), but if the graph is dense we can only reach O(n2/logn).O(n2/logn).
To improve Dijkstra’s simple algorithm, one can make an implementation of k-ary heaps as proposed by Johnson. Fredman and Tarjan further improve the complexity by using a Fibonacci heap.
See references for more information.
References
- Fundamentals of algorithmics by G. Brassard and P. Bratley
- Princeton University, Dijkstra’s algorithm and Bellman-Ford algorithm
- scipy.sparse.csgraph.dijkstra library
- Arbitrage Strategy using Negative Cycle Detection Algorithm
- Currency aribitrage detection
Stay tuned for the next installment in which Mario Pisa will discuss use the Dijkstra algorithm.
Visit QuantInsti for additional insight on this topic: https://blog.quantinsti.com/dijkstra-algorithm/
Disclosure: Interactive Brokers Third Party
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from QuantInsti and is being posted with its permission. The views expressed in this material are solely those of the author and/or QuantInsti and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.
Disclosure: Forex
There is a substantial risk of loss in foreign exchange trading. The settlement date of foreign exchange trades can vary due to time zone differences and bank holidays. When trading across foreign exchange markets, this may necessitate borrowing funds to settle foreign exchange trades. The interest rate on borrowed funds must be considered when computing the cost of trades across multiple markets.














Join The Conversation
For specific platform feedback and suggestions, please submit it directly to our team using these instructions.
If you have an account-specific question or concern, please reach out to Client Services.
We encourage you to look through our FAQs before posting. Your question may already be covered!