Background on sets
A set in Python is an unordered collection of unique elements. Sets are mutable and iterable (more on these properties later). Sets are useful for when dealing with a unique collection of elements – e.g. finding the unique elements within a list to determine if there are any values which should be present. The operations built around sets are also handy when you need to perform mathematical set-like operations. For example, how would you figure out the common elements between two lists? Or what elements are in one list, but not another? With sets, it’s easy!
How to create a set
We can define a set using curly braces, similar to how we define dictionaries.
nums = {10, 20, 30, 40, 50}We can confirm that nums is indeed a set by using the type function:
type(nums)
We can also convert a list to a set like this:
some_list = [1, 2, 3, 4, 5] some_set = set(some_list)
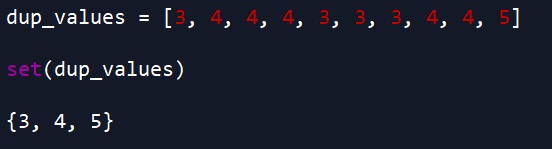
By wrapping our list inside set, we can coerce our list into a set. Also, since sets contain only unique elements (e.g. no duplicates), if we convert a list containing duplicate values to a set, the set will give us just the unique elements.
dup_values = [3, 4, 4, 4, 3, 3, 3, 4, 4, 5] set(dup_values)
How to test if two sets are equal
We can test if two sets are equal using the normal “==” operator.
other_nums = {30, 10, 50, 40, 20}
other_nums == nums # returns True
nums == {20, 30} # returns FalseNotice – since sets are unordered, it doesn’t matter that the set other_nums looks like its elements are in a different order. Set equality comparison just takes into account if the two sets share the exact same elements, regardless of order. And that brings us to the next point – there’s no indexing with sets. This means there’s no such thing as the “first” element or “second element”, etc. in a set (unlike a list). Each set is a just a container of unique, unordered elements.
Combining sets
To combine, or take the union of sets, we use the union method:
others = {60, 70, 80}
combined = nums.union(others)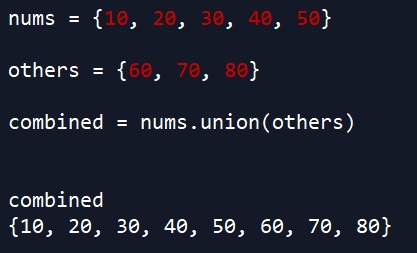
Adding elements to sets
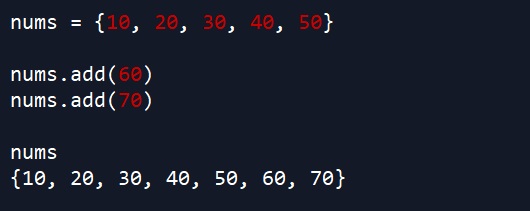
To add an element (or elements) to a set, we use the add method.
# add 60 to nums set nums.add(60) # add 70 to nums set nums.add(70)
Getting the intersection of two sets
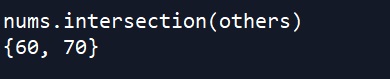
To get the intersection, or what common elements exist between two sets, we use the intersection method.
nums.intersection(others)
Now, what if we want to find the common elements between two lists, rather than sets? All we have to do is convert our lists to sets, and we can use the same intersection method.
list1 = [4, 5, 5, 6, 7]
list2 = [5, 7, 8]
set(list).intersection(set(list2)) # returns {5, 7}How to get the difference between two sets
We can get the difference between two sets (i.e. what elements exist in one set, but not the other) using the difference method.
nums.difference(others)

Just like getting finding the common elements between lists with the intersection method, we can find what elements belong in one list, but not another by converting the lists into sets and applying the difference method. For example, the below code will return {1, 2} because 1 and 2 are each present in list1, but not list2.
list1 = [1, 2, 3, 4]
list2 = [3, 4, 5]
set(list1).difference(set(list2)) # returns {1, 2}How to get the symmetric difference between two sets
The symmetric difference between two sets, A and B, are the set of elements that exist only in A, or only in B. We can illustrate with our example sets.
nums.symmetric_difference(others)

Adding a set of elements to another set
Using the add method above, we can add one element at a time to a set. But what if we want to add a full set of other elements at once? We can do that using the update method. This method is inplace, which means we don’t need to assign a variable to the new result. Instead, calling nums.update(SOME SET GOES HERE) will update the value of nums to include whatever elements are in the input set. We can see this in the example below by updating nums to include the elements in the letters set that we define.
letters = {"a", "b", "c"}
nums.update(letters)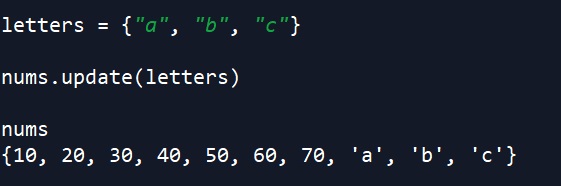
If we want to take out these new elements, we can just use the previously mentioned difference method.
nums = nums.difference(letters)
How to tell if two sets contain no common elements (disjoint)
Python has several Boolean methods available for sets. For instance, we can check if two sets are disjoint (i.e. they do not share any common elements) by using the isdisjoint method.
nums.isdisjoint(letters) # returns True
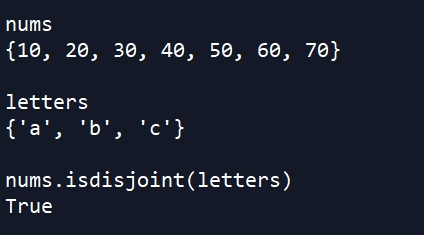
{"a", "d"}.isdisjoint(letters) # returns FalseChecking if a set is a subset of another
sample = {"a", "c"}
sample.issubset(letters) # returns True
sample.issubset(nums) # returns False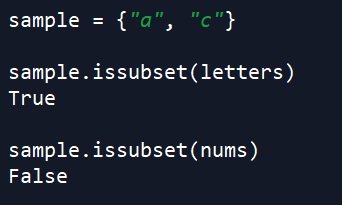
Checking if a set is a super set of another
Similarly, we can also test if a set is a super set of another (i.e. A is a super set of B if every element in B is also in A, which also means that B must be a subset of A). In this case we use the superset method.
sample = {"a", "c"}
letters.issuperset(sample) # returns True
letters.issuperset(nums) # returns False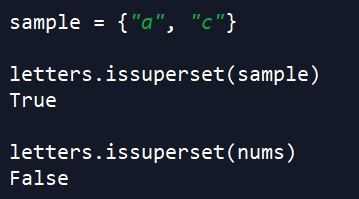
How to remove a single element from a set
Removing a single element from a set can be done a couple of ways. One way is using the discard method. This method will not raise an error if the element to be removed is not actually present in the set. The discard method is inplace.
mixture = {"a", "b", 1, 2, 3}
# after running this line
# mixture no longer contains "a"
mixture.discard("a")
# nothing happens to mixture
# since the string "something" is not present
# in the set
mixture.discard("something")A single element can also be removed from a set using the remove method. The difference here is that the remove method will raise an error if the element to be removed is not present in the set.
# remove "b" from set
mixture.remove("b")
# try to remove "something"
# from set
mixture.remove("something") # error occursSets are mutable
Mutable means that an object can be changed after it is instantiated. Thus, if we create a set, we can change its contents without formally re-defining the set. We’ve already seen examples of this above. For example, consider again adding an element to a set.
# add 60 to nums set nums.add(60) # add 70 to nums set nums.add(70)
Here, we didn’t have to re-define nums. We’re allowed to add an element to the set we’ve already created because of the fact that sets are mutable. If sets were not mutable, we would not be able to do this. To learn more about mutability, see here.
Sets are iterable
Sets are also iterable, which means we can loop over the elements of any set.
test = {4, 5, 6, 7, 8}
# print each element in test
for num in test:
print(num)Set comprehensions
Python also supports set comprehensions, which are very similar to list comprhensions, except they use sets instead of lists for their base construct. Check out the tutorial on list comprehensions, and you’ll be able to apply the same concepts to set comprehensions.
Set comprehensions allow you to create a set by looping through either another set or some other object. For example, below we’re able to create a set where every element is two times the elements in the original set, test. This is done my looping through each element in test (calling each element here “num”), and returning num * 2 i.e. the element times two.
test = {4, 5, 6, 7, 8}
# multiply every element in test by 2
{num * 2 for num in test}Just like list comprehensions, set comprehensions also support looping and filtering in one step. Below we loop through each element in test and output that element to a new set if the element is less than 6 (“num < 6”).
# get the subset of test where each number is less than 6
{num for num in test if num < 6}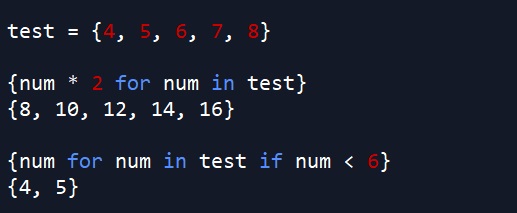
Originally posted on TheAutomatic.net blog.
Disclosure: Interactive Brokers Third Party
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from TheAutomatic.net and is being posted with its permission. The views expressed in this material are solely those of the author and/or TheAutomatic.net and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.
















Join The Conversation
For specific platform feedback and suggestions, please submit it directly to our team using these instructions.
If you have an account-specific question or concern, please reach out to Client Services.
We encourage you to look through our FAQs before posting. Your question may already be covered!